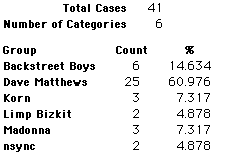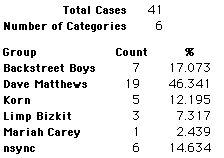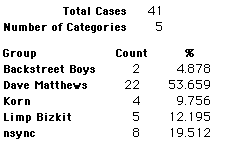
We examined specific contexts to address whether an observed event should be considered "unusual". By unusual we meant, "Do random events like this one happen a relatively small fraction of the time under the conditions we've assumed?"
For example, "Is it unusual that a random sample of 12 skates has two or more defective skates (this is the observed event) if, as the manufacturer claims, only 4 of every 500 skates are defective (this is the assumed circumstances)?"
We used ProbSim to generate large numbers of samples taken from populations that we assumed had well-defined characteristics. The characteristics we assumed often came from someone's claim about the population (e.g., a manufacturer's claim about the fraction of skates they produce that have defective wheels).
If, by generating a large number of repetitions, we saw that events like the one actually observed are relatively rare with respect to the population as we'd assumed it, then we concluded that the assumptions and the observed event are discrepant. THAT IS, we cannot conclude that the assumptions are wrong. Rather, we can conclude only that the assumptions and the observed result cannot be reconciled.
In this example, it was relatively rare to get random samples that have 2 or more defective skates when we select 12 skates at random from a population of skates having just 8/1000 of them bad. (About 1 sample in 100 will have two or more bad skates under those conditions.)
But we DID see a sample that had 2 of 12 skates being bad. Something doesn't jibe. However, we have TWO assumptions, either of which that could be problematic:
One of those assumptions is suspect, but we cannot determine which one is the culprit without having someone find out some facts about the situation (e.g., the ACTUAL method of gathering their sample).
If we were to decide that the sampling procedure was good, then we must question the assumption about the population. But we would first have to determine (or just accept) that the sampling procedure was good.
In one two week we will begin studying "good" procedures for actually collecting samples.
In the mean time ...
We will explore this question:
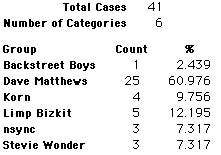
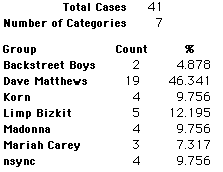
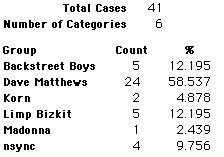
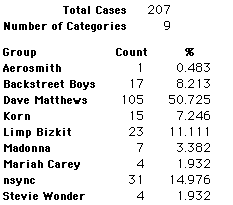
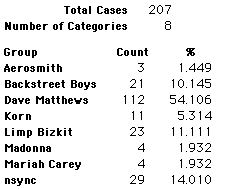
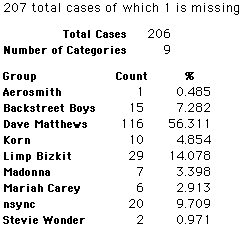
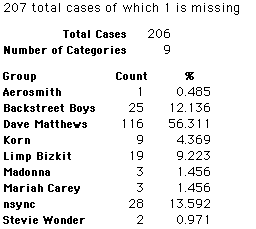
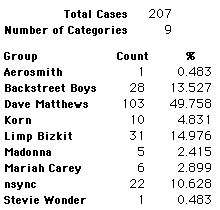
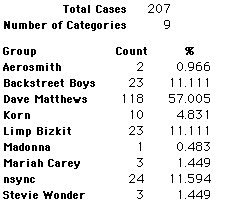
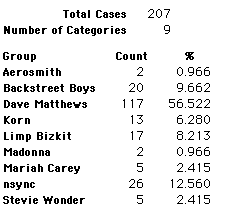
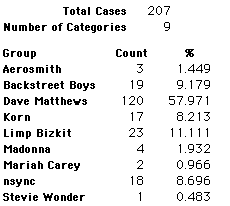
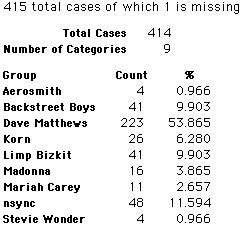
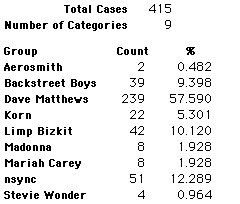
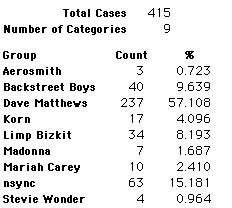
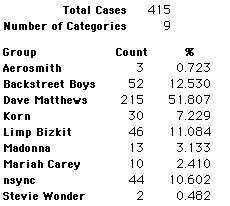
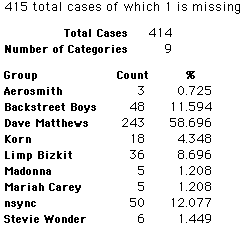
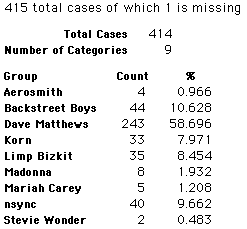
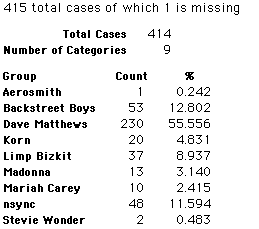
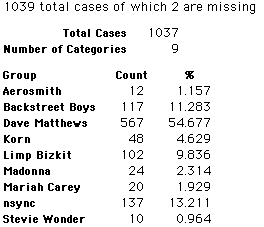
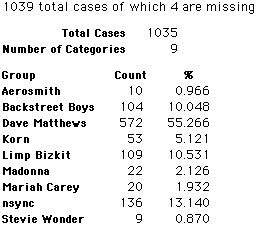
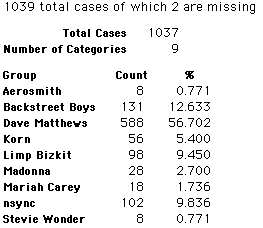
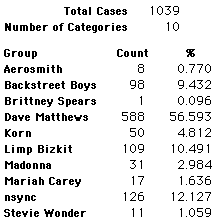
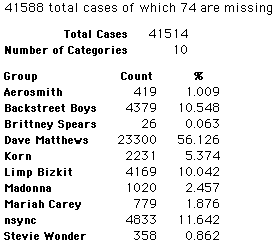
A group of 41,588 high school students were asked to select their favorite from among 10 performers. The performers were presented in a list. Students had to select from that list.
Each student made just one choice. Here are their choices. (74 students left their forms blank.) The table shows that 419 students, or a little more than 1% of the students, selected Aerosmith; about 10.5% of the students selected Backstreet Boys.

We will accept these opinions as fact. CONSIDER THESE RESPONSES AS A POPULATION. DO NOT CONSIDER THEM AS A SAMPLE.
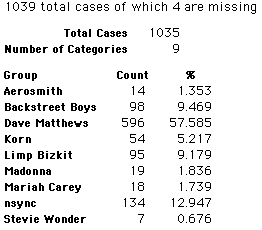
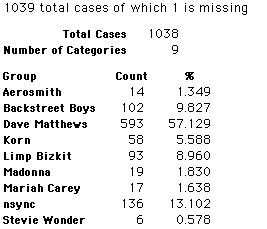
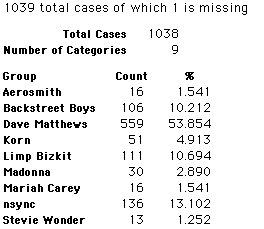
In this activity we will randomly select samples from this population and compare the samples with the population to see how representative the samples are. We will do this with samples of size 40, 200, 400, and 1000. For example, we will randomly select 20 questionnaires from the 41,588 questionnaires and then examine the percent of the sample choosing Aerosmith, the percent of the sample choosing Backstreet Boys, and so on.
Compare those percentages with the actual population percentages given above. To do this, it might be helpful to organize the comparison in a table, like this:
| 40 Stu's | Actual | Samp1 | Samp2 | Samp3 | Samp4 | Samp5 | Samp6 |
| Aerosmith |
1.00 | ||||||
| Backstreet Boys | 10.55 | ||||||
| Brittney Spears | 0.06 | ||||||
| Dave Matthews | 56.13 | ||||||
| Korn |
5.37 | ||||||
| Limp Bizkit | 10.04 | ||||||
| Madonna |
2.46 | ||||||
| Mariah Carey | 1.88 | ||||||
| nsync |
11.64 | ||||||
| Stevie Wonder | 0.86 |