Discussion of Quickie Question #2

BHStat

September 3, 1999

Discussion of Quickie Questions 2

What criterion do we use to determine that percents calculated from samples of one size tend to be more accurate than percents calculated from samples of another size?

This question turns out to have been phrased poorly.
  It would have been better to ask, "How do we tell that one
  collection of sample percents is more accurate than another?"
  This would have made clear that sample size is not the real issue;
  rather,assessing accuracy is the real issue. As such, one collection
  of sample percents is more accurate than another if samples in
  it tend to deviate less from the population percent than does
  the other collections' percents.

Several of you understood this question to be "what
  happens to accuracy as we use samples of larger sizes?"
  That is a good question, but an answer to it does not answer
  the question of how we determine that one collection is
  more accurate than another.

What did Dr. Thompson mean when he said, "We reach a point of diminishing returns" when we try to increase sampling accuracy by making sample sizes larger and larger.
Several of you were right on target -- that if we are in the process of planning to collect a sample to find out something about a population, the larger the sample we plan the more we are assured of accurate results. However, at some point, the increased expense of taking a larger sample does not produce a proportionate increase in accuracy, and at some point later point yet the increased expense of taking a yet larger sample hardly produces any increase in accuracy.
The histogram below shows the simulated results of drawing 2000 samples of 500 marbles from a jar having a gazillion marbles in it, 57% of which were red.

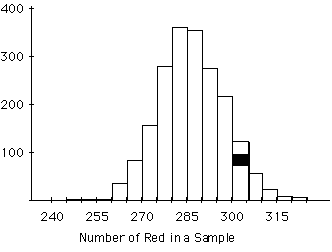
a) What does "285" on the horizontal axis stand for?

It stands for 285 red marbles in a sample

b) What does "100" on the vertical axis stand for?

It stands for 100 samples having a number of red marbles within some interval

c) What is represented by the highlighted slice of the bar above 300-305?

It stands for a subgroup of all the samples that had 300, 301, 302, or 304 red marbles in them.