BHS Statistics
September 7, 1999
The key to this assignment was to GO SLOW in reading the column labels. "% of Sample Percents" refers to a fraction of the collection of samples that were drawn repeatedly from some population.
The phrase "... within x percentage points of the population percent" refers to a range surrounding the population percent. In the first example, the population percent was .57 (57%). Therefore, for a sample to be within 1 percentage point of the population percent, it would have to have a percent saying yes that is between 56% and 58%.
For example, with regard to the first histogram:


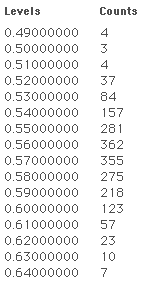
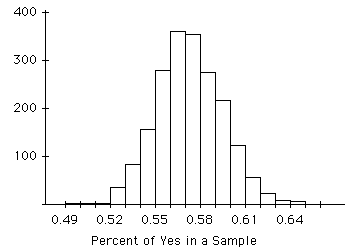
2000 Samples of 500 each taken from a population having .57 of it believing "yes".
Analysis: There are 2000 samples. The population percent is .57 (i.e., 57% of the population believes "yes"). Any sample having a percent saying yes between .56 and .58 will be within 1 percentage point of the population percent. 362 of the samples had percentages between .56 and .57; 355 of them had percentages between .57 and .58. Therefore, 717 of these 2000 samples, or approximately 36%, were within 1 percentage point of the population percent.
And so on for the rest of the tables.
| Percent of Yes in Population | Number of Samples Drawn | % of Sample Percents within 1 Percentage Point of Population % | % of Sample Percents within 2 Percentage Points of Population % | % of Sample Percents within 3 Percentage Points of Population % | % of Sample Percents within 4 Percentage Points of Population % |
| 57% | 2000 |
36% |
64% |
82% |
93% |
| 60% | 2000 |
36% |
65% |
85% |
93% |
| 65% | 2000 |
37% |
65% |
85% |
95% |
| 32% | 3000 |
37% |
66% |
85% |
94% |