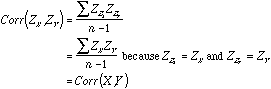I presented these ideas in such a rush that I made several mistakes. Here is a better version.

1. Reminder of definitions
   
   
   1. Variables are characteristics of cases on which we gather information. So, variables are things like
      
      
      1. people’s opinions on a current topic (case -- person, characteristic -- opinion)
      2. sharpness of the knives a company produces (case -- knife, characteristic -- sharpness)
         
         

      So, if we are interested in cities’ liveability, we would gather information on a number of characteristics, such as cities’ climate, economy, crime rates, etc. In this situation, each city is one case. Climate, economy, crime rate, etc. are variables. The actual measures gotten for any city are that city’s values on the variables.

   2. A variable’s mean is denoted with a bar over its letter (e.g., 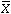). A variable’s variance is denoted by 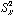; its standard deviation, the square root of the variance, is denoted by the letter s and the variable’s letter as a subscript (e.g., ).
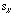   3. If X is a variable, then the mean is calculated as 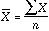(the sum of the values of X divided by the number of values of X).
   4. If X is a variable, then the variance S² is calculated as 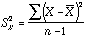(the sum of the squared differences between values and the mean, divided by one fewer than the number of cases).
   5. A variable’s standard deviation, denoted s_X is calculated as the square root of its variance. So a variable’s standard deviation is
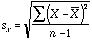
   6. If X is a variable, then the set of z-scores derived from X is calculated by .

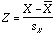      That is, each value of X is changed by subtracting the variable’s mean from it and then dividing that difference by the standard deviation. Put another way, a scores Z-score is its number of standard deviations away from the variable’s mean.

2. If any variable X has n values whose mean is and standard deviation , then the set of z-scores gotten from X has mean 0 and variance 1.

                

    

3. The z-score of a z-score is itself.

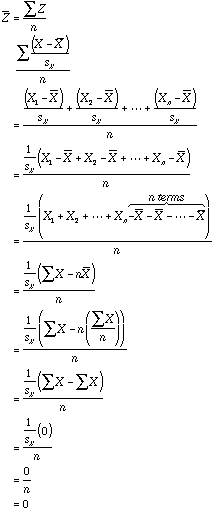
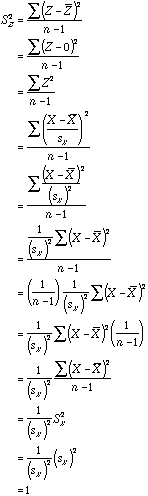
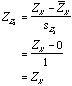
   Notice that this fact is a direct consequence of z-scores having a mean of 0 and a variance of 1.

    

4. The correlation between two variables X and Y is the same as the correlation between Z_X and Z_Y. That is, converting variable’s values to z-scores does not affect their correlation.

Notice that this fact is a direct consequence of the fact that the z-score of a z-score is itself.