Expected Value (Defined)

Suppose you have a probabilistic situation such that every outcome has a numeric value. The expected value of that process is the value per repetition you would expect over the long run. For instance, suppose some process is repeated 2 million times, and that the sum of the values of those two million outcomes is 5,338,792. Then the value per repetition of this process, for those 2 million repetitions, is

Note: This is not to say that when determining a process’s expected value you are predicting what will actually happen in any number of repetitions. Rather, you are stating what you expect to happen, knowing that actual long-term average values will depart somewhat from the expected value.

BHS Statistics

March 31, 2000

Expected Value

What is the expected value of games like this, assuming that the coach tells Pedro to stay on first?

What is the expected value of games like this, assuming that the coach tells Pedro to attempt to steal second?

Do you think the coach should tell Pedro to steal?

BHS Statistics

March 31, 2000

At the Cobb County fair a clown is sitting at a table with three cards in front of her. She shows you that the first card is red on both sides, the second is white on both sides, and the third is red on one side and white on the other. She picks them up, shuffles, hides them in a hat, then draws out a card at random and lays it on the table, in a manner such that both of you can see only one side of the card. She says: "This card is red on the side we see. So it’s either the red/red card or the red/white card. I’ll bet you one dollar that the other side is red."

Assuming you take the bet, what is this game’s expected value?

(A point of clarification: To take her bet would be to wager that the card in question is red/white.)

Please do all your work on a separate sheet of paper. Write in complete sentences and paragraphs.

BHS Statistics

March 31, 2000

Expected Value

Background

In the Yakima Valley, Washington State’s largest apple-growing region, farmers face a major threat from frost during the time the trees have blossoms. The blossoms are killed when frost forms on them and, as a result, the tree is incapable of being pollinated. In other words, if frost forms on the blossoms on a branch, that branch does not produce any fruit that year. (However, typically only 1/5 of a tree’s branches is damaged on a frosty night.)

To protect his trees from frost, a farmer puts hundreds of "heaters" (tall metal contraptions that are like chimneys sitting on top of reservoirs of diesel fuel) in the orchard. Burning them all night can raise the temperature just above the frost point and save his crop.

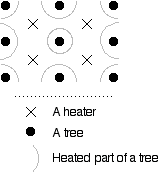
However, to be effective, the farmer must light the heaters well before the temperature drops below the frost point. He must therefore guess as to whether the temperature on any night will actually drop low enough to damage his crop. He has lit the heaters needlessly on more than one occasion — the temperature never got below the frost point.

One heater protects a total of 1 tree (see diagram).

It costs a farmer $150 per heater per night when he lights his heaters.

It costs a farmer $380 per tree per night if the temperature goes below the frost point. So a farmer gains $380 per night (minus expenses) if he saves a tree from frost.

Situation

You are on a Farmers Co-operative task force. This task force has been charged with the responsibility of producing guidelines for when farmers should use heaters. The committee decided to make it simple by handing out the following chart completed with "heat" or "don’t heat" on each line.

Fill in the table. Prepare a report for members of the Farmers Co-op that explains how you arrived at your recommendations.