Brentwood High School
Vanderbilt University
Conceptual Statistics Project
Probability Exam, Part I
This exam is in two parts. If you finish the first part
on Day 1, then you may begin Part II.
Please do all your work on this exam. Use the blank sheets
provided by us if you need more room. Do not combine work from different problems
on one sheet. Use different blank sheets for different problems.
Be sure to ask for clarification whenever necessary!
If we cannot answer your question without telling you what to write, then we
will say so. Otherwise, we will do our best to clarify the question.
SHOW YOUR WORK so that we may give you partial credit wherever
you’ve earned it. An incorrect answer with no work or without explanation
is compltely incorrect. An incorrect answer with work that shows valid reasoning
but poor arithmetic is mostly correct.
PLEASE WRITE CLEARLY AND LEGIBLY. We cannot grade what we
cannot read! We will monitor the class as you take the exam and let you know
when we cannot read your writing. But it is your responsibility to ensure we
can read what you’ve written.
DO NOT attempt to say what you think we want to hear. Answer
each question with your very best reasoning. We can tell the difference.
Good work!
- You must make a choice between:
- Definitely receiving $225
- A 25 percent chance of winning $1,000 and a 75 percent
chance of winning nothing
- Suppose this is a one-time choice.
That is, you are presented with these options once and you will never be
presented with these options again. Would you choose (i) or (ii)? Why?
- Suppose you are a gambler who will be presented
with these same options many, many times. Would you choose (i) or (ii)?
Why?
- You must make a choice between:
- Definitely losing $700
- A 75 percent chance of losing $1,000 and a 25 percent
chance of losing nothing
- Suppose this is a one-time choice. That is, you
are presented with these options once and you will never be presented
with these options again. Would you choose (i) or (ii)? Why?
- Suppose you are a gambler who will be presented
with these same options many, many times. Would you choose (i) or
(ii)? Why?
- An urn contains two white balls and two black balls.
Two balls are drawn, without replacement.
- What fraction of the time will you select a white ball
on your second choice given that you selected a white ball on your first
choice?
- What is the probability that the second ball is white
given that the first ball is black?
- What is the probability that the first ball is white
given that the second ball is white?
- Linda is 31, single, outspoken, and very bright. She
majored in philosophy in college. As a student, she was deeply concerned with
discrimination and other social issues, and participated in anti-nuclear demonstrations.
Is statement (i) or statement (ii) more likely to be true? Why?
- Linda is a bank teller
- Linda is a bank teller and active in the feminist
movement
Answer:
Reason:
- Draw tree diagrams for these situations. Label each branch
with the fraction of the time its outcome will happen at that stage of the
process.
- Form a 3-person committee from a group that consists
of 4 males and 2 females
Tree diagram:
What is the probability the committee has 2 females?
- A game show host places a prize behind one of three
doors. You choose one of the three doors. The game show host opens one of
the remaining doors to show the prize was not behind it. You then switch
doors.
Tree diagram:
What is the probability that you win the prize?
- Each year Vanderbilt University
compiles data on its student population, which it then reports in the weekly
newspaper, The Vanderbilt Hustler. In 1999 the Hustler reported the
following facts:
- 12% of students majored in natural science.
- 36% of students were from the South.
- Of students from the South, 11.9% were natural
science majors.
- Of students from Tennessee, 4% were natural science
majors.
- Convert each of the reported percentages into a probability
statement.
Suppose you were to select students at random from the
1999 Vanderbilt student population.
- What is the probability that a student majors in natural
science and is from the South?
- Given that a student is from the South, what is the
probability that she/he is not a natural science major?
- Given that a student is from Tennessee, what is the
probability that she/he is not a natural science major?
- Are the events student majors in natural science
and student is from the South independent? Explain.
Brentwood High School Vanderbilt University Conceptual
Statistics Project Probability Exam, Part II
This is the second part of this two-part exam.
Please do all your work on this exam. Use the blank sheets
provided by us if you need more room. Do not combine work from different problems
on one sheet. Use different blank sheets for different problems.
Be sure to ask for clarification whenever necessary!
If we cannot answer your question without telling you what to write, then we
will say so. Otherwise, we will do our best to clarify the question.
SHOW YOUR WORK so that we may give you partial credit wherever
you’ve earned it. An incorrect answer with no work or without explanation
is compltely incorrect. An incorrect answer with work that shows valid reasoning
but poor arithmetic is mostly correct.
PLEASE WRITE CLEARLY AND LEGIBLY. We cannot grade what we
cannot read! We will monitor the class as you take the exam and let you know
when we cannot read your writing. But it is your responsibility to ensure we
can read what you’ve written.
DO NOT attempt to say what you think we want to hear. Answer
each question with your very best reasoning. We can tell the difference.
Good work!
- You have a torn tendon and are facing surgery to repair
it. The surgeon explains the possible complications to you: infection occurs
in 3% of such operations, the repair fails in 14% of the operations, and both
infection and failure occur together in 1% of the operations.
- What percent of these operations succeed and are free
from infection?
- Draw a diagram that shows how you determined this percentage.
- Consider the following question:
"What is the probability that a surgery like this
is without infection or failure?"
Is this question the same or different from question (a)?
Explain your answer.
- The American Journal of Public
Health (July 1995) published a study on unintentional carbon monoxide
(CO) poisoning of Colorado residents. A total of 981 cases of CO poisoning
were reported during a six-year period. Each case was classified as fatal
or nonfatal and by source of exposure. The number of cases occurring in each
of the categories is shown in the data table.
|
Source of Exposure
|
Fatal
|
Nonfatal
|
Total
|
|
Fire
|
63
|
53
|
116
|
|
Auto exhaust
|
60
|
178
|
238
|
|
Furnace
|
18
|
345
|
363
|
|
Kerosene or spaceheater
|
9
|
18
|
27
|
|
Appliance
|
9
|
63
|
72
|
|
Other gas-powered motor
|
3
|
73
|
76
|
|
Fireplace
|
0
|
16
|
16
|
|
Other gas-powered motor
|
3
|
19
|
22
|
|
Unknown
|
9
|
42
|
51
|
|
Total
|
174
|
807
|
981
|
Suppose you were to select cases at random from these
981 cases of unintentional CO poisoning.
- Let A be the event that a selected case had fire as
its poisoning source, and let B be the event that the case is fatal.
- What does the symbol "A|B" mean in this
situation?
- What does "P[A|B]" stand for?
- Determine P[A|B]. (That is, determine its actual
numeric value.) You need not calculate. You may write probabilities as
fractions, such as
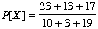
.
(Question 8, continued. You need not calculate
when answering a question. You may write probabilities as fractions, such
as 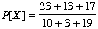 ).
).
- Given that a case is nonfatal, what is the probability
that it is caused by auto exhaust?
- What is the probability that a case is nonfatal and
caused by auto exhaust?
- What is the probability that a case having an unknown
source is fatal?
- If a case is nonfatal, what is the probability that
the source is not fire or a fireplace?
- A certain town is served by two hospitals. In the larger
hospital about 45 babies are born each day, and in the smaller hospital about
15 babies are born each day. Although the overall proportion of boys is about
50 percent, the actual proportion at either hospital may be greater or less
than 50 percent on any day. At the end of a year, which hospital will have
the greater number of days on which more than 60 percent of the babies born
were boys?
- the large hospital
- the small hospital
- neither –the number of days will be about the same
(within 5% of each other)
- Your choice:
- Why you made your choice:
- US Steel Corporation manufactures steel beams, among
other products. A good steel beam has uniform density all along its length
(this guarantees that it has uniform strength – no weak spots). US Steel
has a very expensive (and completely accurate) test that x-rays the entire
beam. Using this test, they determined that approximately 1% of the beams
they produce are faulty.
They want to use a much cheaper sonogram test. They’ve
determined that the sonogram test is 98% accurate – it is right 98% of
the time.
- What fraction of the beams that the sonogram says are
bad are actually bad?
- US Steel gains $25000 when they send out a good beam
and they lose $3000 (for return shipping and handling) when they send out
a bad beam. What is US Steel’s expected value per beam when using the
sonogram test?
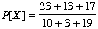
![]() ).
).