Test 2

Please do all your work on this test. Use a PENCIL; do not use a pen. Write in complete sentences and express yourself clearly. Be precise, yet concise.

Use the extra sheets at the end of the test if you need extra space. Be sure to label your work on the extra sheets with the problem number it goes with.

Good luck! Do a good job!

1. General Motors divisions (Chevrolet, Buick, Oldsmobile, etc.) manufactured approximately 35% of all automobiles owned in Middle Tennessee. One morning, while sitting at a red light, Brady noticed that the 5 cars around him (1 in front, 3 aside, 1 in back) were all GM automobiles.
   
   1. What would it mean for this event to be "statistically unusual"?

       

       

       

       

       

       

       

       

   2. How would you investigate whether this event is, in fact, statistically unusual?

    

    

    

2. The histogram and table below show the simulated results of selecting 10,000 random samples of 1024 people, each sample taken from a large population of which .40 believe "yes" on some subject.
   
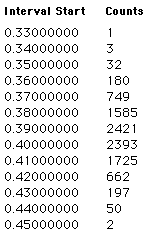
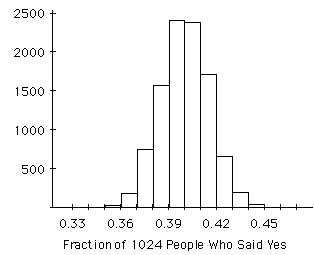
   1. What does "0.38" stand for in the column under "Interval Start"?

       

       

       

       

   2. What does "50" stand for under in the column under "Counts"?

       

       

       

       

   3. We are going to simulate collecting 3000 random samples of size 1024 people, but from a population of which .60 believes "yes". Approximately what fraction of those samples will have between .59 and .61 of the people in them believing "yes"?
      
      
      
3. Here is a table similar to one we filled out in an in-class activity. Use it in answering parts a through e.

   Percent of Yes in Population	Number of People in a Sample	Number of Samples Drawn	% of Sample Percents within 1 Percentage Point of Population %	% of Sample Percents within 2 Percentage Points of Population %	% of Sample Percents within 3 Percentage Points of Population %	% of Sample Percents within 4 Percentage Points of Population %
   65%	500	2500	36.7%	64.5%	84.8%	91.5%
   32%	500	2000	37.1%	65.8%	83.9%	91.1%
   57%	500	6800	36.2%	64.9%	84.2%	91.3
   60%	500	5500	36.1%	65.2%	84.3%	91.4%

   1. To how many populations does this table refer?

       

   2. The entry in column 5, row 3 is 64.9%. That refers to 64.9% of what (be specific)?

       

   3. The entry in column 1, row 4 is 60%. That refers to 60% of what (be specific)?

       

   4. All the percents in each of columns 4 through 7 are approximately the same. What can we conclude from that?

       

       

       

   5. Stan's statistics class was discussing a Gallup poll of 500 TN voters' opinions regarding the creation of a state income tax. The poll stated, "… the survey showed that 36% of Tennessee voters think a state income tax is necessary to overcome future budget problems. The poll had a margin of error of ±4%."

   Stan said that the margin of error being 4% means that between 32% and 40% of TN voters believe an income tax is necessary.

   Is Stan's interpretation a good one? If so, explain. If not, what should it be?

    

4. The Harris and Gallup companies are well known for conducting public opinion polls in America. Typically, they make a claim about what some population believes on a subject and base that claim on one sample drawn at random from that population.