Explaining Oneself

Types of Explanations

There are many types of explanations, but there are extreme forms along a continuium from completely procedural, stating only what you have done, to highly sophisticated and rich with implications, stating the necessary principles at play but not saying how those principles underly what you did. We will call the first extreme a Procedural explanation (all the steps but no insight). We will call the second extreme a Conceptual explanation (all insight without directions). We will aim for Reasoned explanations -- less extreme than a purely conceptual explanation but certainly in the conceptual neighborhood. A reasoned explanation is one that is rich with imagery, motives, and implications AND spells out their connections with the task at hand.

Example

Problem:

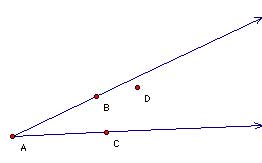Given angle BAC and point D internal to BAC, construct a circle that is tangent to rays AB and AC and which contains point D.

Procedural Explanation:

1. Construct ray k, the bisector of angle BAC.
2. Construct ray AD.
3. Let point R be a point on k.
4. Construct line m, the line perpendicular to AB through R.
5. Construct point S, the intersection of side AB and m.
6. Construct the circle centered at R and passing though S (circle RS).
7. Construct point T, the intersection of ray AD and circle RS.
8. Construct segment RT.
9. Construct line c, passing through point D parallel to segment RT.
10. Construct point U, the intersection of line c and ray k.
11. Construct the circle centered at U passing through D. This circle will be tangent to rays AB and AC.

Reasoned explanation.

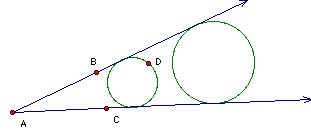Suppose we have another circle C1 that is tangent to rays AB and AC. Then:

• the target circle (the one passing through D) is a scaled version of C1
• both circles will be centered on the angle bisector of the angle
• If we let point T be the intersection of ray AD and circle C1, then the segment connecting T and the C1's center R will be parallel to the segment connecting D and the target circle's center U.
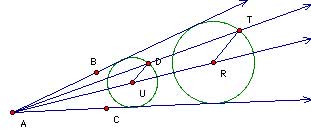• So, to get the target circle:
  • Construct any circle C1 that is tangent to the angle's sides. Let R be C1's center.
  • Construct ray AD and find an intersection T between it and circle C1
  • Connect T and the C1's center R.
  • Construct a line c parallel to TR through D
  • Find the intersection U of c and the angle bisector. U is the center of the circle passing through D that is tangent to the angle's sides.