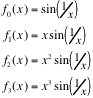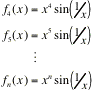Please be brief but clear in your answers to each of the following. Be alert to going back to the fundamental meanings of angle measure, sin( ), and cos( ) whenever it will help to construct a coherent explanation.
1.
Graph sin(x), -10 < x < 10; answer a-d.
a)
What does x stand for?
b)
What does "sin(x)" mean for some specific value of x?
c)
What does a point on the cartesian graph of sin(x) stand for?
d)
Why does the cartesian graph of sin(x) appear as it does?
2.
Jimmy said, "I found a neat trick. sin( ) has a period of 2pi, which means that it repeats itself whenever whatever is in the parentheses varies by 2pi. So, sin(5+3x) is periodic whenever 5+3x varies by 2pi."
3.
Explain the behavior of y = a sin(x) in a way that, with very little modification, your explanation also works for explaining the behavior of y = cos(x)sin(x).
4.
Explain the behavior of y = cos(sin(x)). Then use this as the basis for explaining the behavior of