Activity 1. Imagine this. I'm driving my car at 50 mi/hr. I speed up smoothly to 60 mi/hr, and it takes me one hour to do it. About how far did I go in that hour?

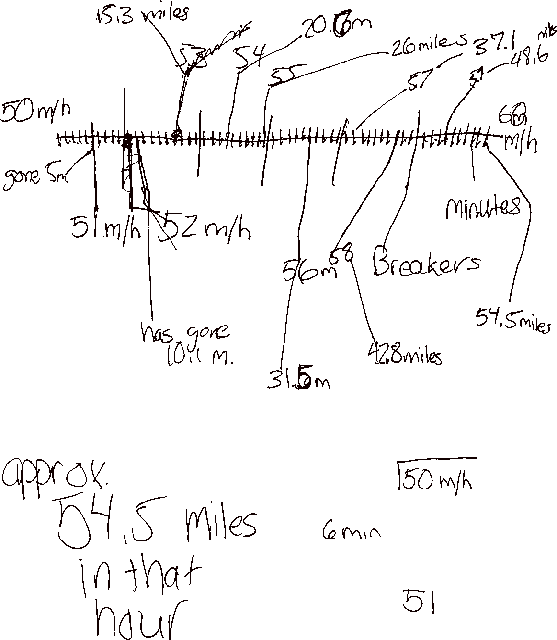
Sue: (Long pause. Begins drawing a number line.)

Pat: What are you doing?

Sue: I figure that if you speed up 10 miles per hour in one hour, that you speeded up 1 mile per hour every 6 minutes. So I'll figure how far you went in each of those six minutes and then add them up.

(In above figure, Sue has represented time and distance on the same number line. Major tickmarked intervals represent elapsed tenths of an hour, and they also represent an increase in speed of 1 mi/hr. Sue assumes I went at a constant speed of 50 mi/hr in the first 1/10 hour, that I went at a constant speed of 51 mi/hr in the second 1/10 hour, and so on. She records her approximation of cumalitive distance at the end of each successive 1/10 hour.)

Pat: (After Sue is finished.) Is this the exact distance I traveled?

Sue: No -- you actually traveled a little farther.

Pat: How could you get a more accurate estimate?

Sue: (Pause.) I could see how far you went every time you sped up a half mile per hour.

Activity 2.

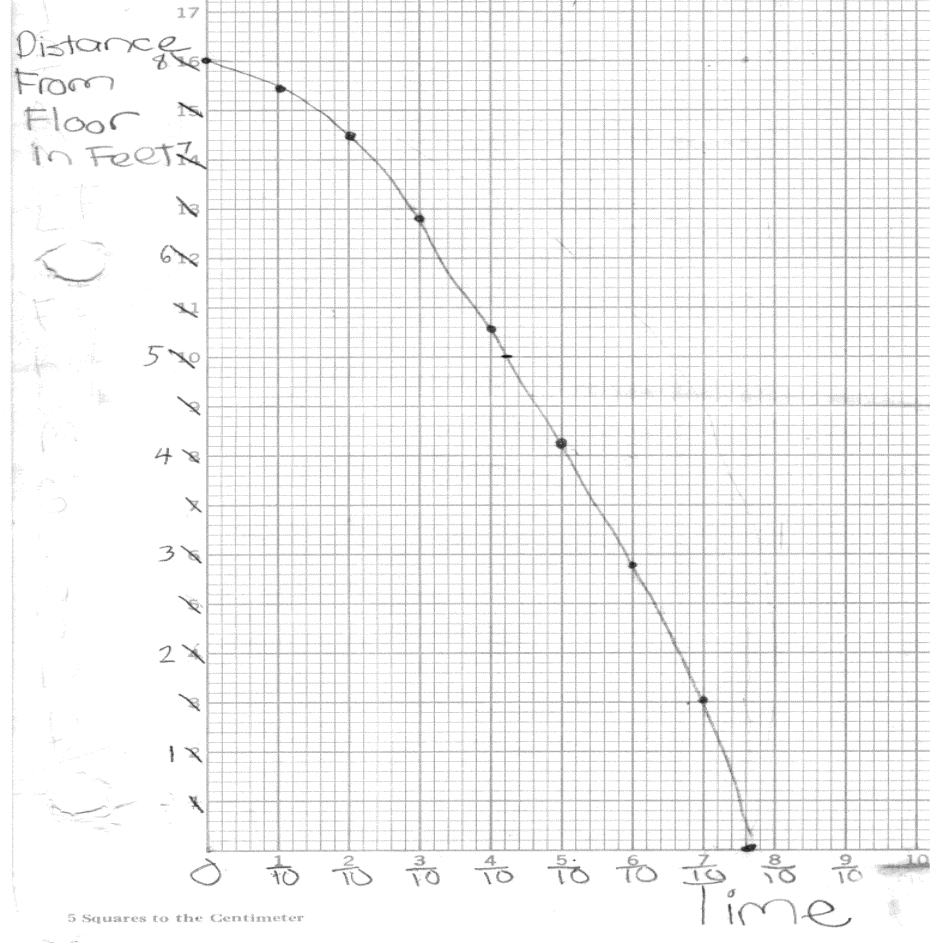
Pat dropped a paper clip several times while standing on a chair and holding it against the ceiling (8 ft above the floor). Daryl and Sue took turns timing its fall with a stop watch.

Pat: About how long does it take to drop?

Kids: Around .76 seconds.

Pat: Does the paper clip fall at the same speed all the time?

Kids: No. It speeds up.

Pat: What does that mean?

Kids: It goes faster each second.

Pat: But it doesn't even fall for one second. How can it go faster each second?

Kids: (Thinking about this for a long time.) It goes faster each tenth of a second.

Pat: Just each tenth of a second?

Kids: Well, no. You could do it for each hundredth of a second if you wanted.

Pat: Okay -- The ceiling is 8 ft above the ground. What is the paper clip's average speed while falling?

Kids: 8 divided by .76 ft/sec (10.53 ft/sec).

Pat: What does this mean? How can it go an average of 10.53 ft/sec if it only goes 8 feet?

Kids: It doesn't need to go 10 feet. It means if it went for one second at this speed it would go 10.53 ft.

Pat: If we dropped it from 10.53 feet, would the paper clip take one second to hit the floor?

Kids: (They're not sure about this. It appears they want to say that it would take one second if it fell at 10.53 ft/sec, but they suspect that it wouldn't have an average speed of 10.53 ft/sec if it were dropped from 10.53 ft.)

Pat: Here's some graph paper. Now, you say that the paper clip speeds up each tenth of a second, and that from 8 feet it will take .76 seconds to fall. This is what I want you to do: Sketch a graph of the paper clip's distance above the ground at each tenth of a second while it is falling. Make sure that your graph has the paper clip hitting the ground in .76 seconds.

Kids: (Their graph is shown below.)