In this assignment you will not be presented with concrete situations to model and interpret. Instead, you are asked to speak about "how fast the value of a function changes with respect to changes in its argument." Think of this as being about an "abstract" situation where there are quantities and units, but they are not given to you.

Functions in this assignment are defined "piecewise." That means that they have one definition over part of their domain and another definition over another part.

I. Investigations

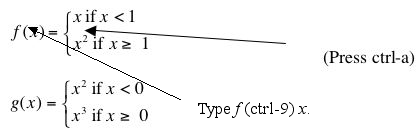
Start with the function . Enter it as y = 1+sin(x) if x<0 (ctrl-a) (tab) cos(x) if x ≥ 0. (See Piecewise Defined Functions in GC.)

Define a function that gives its average rate of change over intervals of length h. Use 2, 1, 0.5, and 0.01 as values of h.

After examinging the average rate of change function: Play the movies below (by double-clicking them), or play with the original GC graph, and then explain why the rate of change function behaves the way it does over large and small intervals.

Use the insights gained here to explain why the average rate function for y = |x| behaves as it does for large and small values of h.

h = 2.0

h = 1.0

h = 0.2

h = 0.05

I. Do the following for each of these two functions:

a. Behavior of the function

Enter the function in Graphing Calculator and graph it by entering y = f (ctrl-9) x or y = g (ctrl-9) x. Note any behavior that merits close scrutiny. Describe the behavior you are scrutinizing and why it interests you.

b. Average rates of change

Enter the definition of a function whose values give the original function's average rate of change over every inteval of length h. Use values of 2.0, 1.0, 0.5, 0.1, and 0.00001 for h. What is going on?

II. Extension - 1

You saw in part I that you can define a function piecewise over an interval. Suppose a function is partially defined as

Experiment by filling in the blank with various polynomials that will continue from 0 where cos(x) stops. Then answer parts (a), (b), and (c) below. When responding to them, simply change the definiton of h. All the functions you define in terms of h will update automatically.

a) Fill in the blank with a polynomial function so that

• h(x) is continuous

• changes smoothly even for extremely small values of h. (Note: enter the definition of k just as it appears here. Graph it by entering y = k (ctrl-9) x.

b) Fill in the blank with a polynomial function so that

• h(x) is continuous,
• k(x) changes smoothly even for extremely small values of h,
• and m(x) = changes smoothly even for extremely small values of h.

c) Generalize

III. Extension - 2

Graph f(x) = x² mod 2 [enter as y = mod(x², 2)]. Then graph the average rate of change function for f using intervals of length 1, 0.5, and 0.001.

Explain what is represented by any point on the average rate function's graph. (Don't say "average rate of change." Say what "average rate of change" means.)

Notice that the graph of f is discontinuous, but that the graph of its derivative (i.e., its average rate of change function over extremely small intervals of change) appears to be continuous. Are appearances deceiving? Explain.