Riemann Sums
1. a. A car accelerates from a standing start at (approximately) the rate of
![]() ,
,
where t is the number of seconds since starting. Use Graphing Calculator and Riemann sums to produce a graph of the approximate velocity (in mi/hr) of the car at each moment during its first 10 seconds of accelerating.
Pick a point on the graph of your function. What are its coordinates? What do its coordinates represent? What does the graph represent?
b. Use Graphing Calculator and Riemann sums to produce a graph of the approximate distance covered (in miles) at each moment during a car's first 10 seconds of accelerating from a standing start when it accelerates at the rate presented in part (a). Use the method that the interval (0,x) is partitioned into n subintervals.
c. Repeat part (b), but use the method that every interval (0,x) is partitioned into subintervals of length d.
2. a. Explain how to think of the expression
![]()
(where p is a fixed number of subintervals) to understand that it defines a function evaluated at every value of x in (a,b)? (Click here for a GC file giving a general definition.)
b. Do functions defined like this
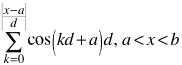
(where d is an arbitrarily small interval size) always produce a step function? If so, why? How does this function differ from the one in (a)? (Click here for a GC file containing a general definition.)
3. Use Graphing Calculator and Riemann sums to produce a graph of the volume of water in a conical storage tank that is 25ft high and 30 feet wide at the top. Express the volume as a function of the height of the water above the tip of the cone.
4. Hexane is a gas used for industrial purposes. Clentice Smith of Cargill Corp., Bloomington, IL requested a graph that will give the approximate volume of hexane (measured in cubic inches) held by the tank shown in Figure 1.* Use Graphing Calculator and Riemann sums to produce such a graph. Express the volume of hexane as a function of the height of the water (measured in inches). A diagram is given on the next page.
Assumptions
• The face of the tank is a disk (i.e., a region bounded by a circle)
• the shape of the tank is cylindrical
• the hexane sits atop the water
• the dimensions of the tank are as shown
• a hole in the tank resides 18" vertically from the top of the tank
• the hexane always reaches the bottom edge of the hole.
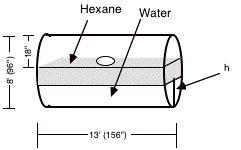
Figure 1
5. a. Find two applications of the integral in a calculus text, not having to do with area or volume, for which these methods are appropriate. Solve them using these methods. (Beware, the answer the textbook seeks will probably be a number instead of a function. So, you will give a more general answer than they request, but you can still answer their question.)
b. Discuss how the question might need to be changed and how the situation might need to be re-framed to make Riemann sums a reasonable method.