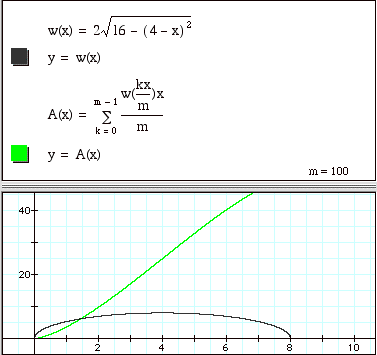
A venetian blind (made of horizontal strips) hangs over a circular window that is 8' in diameter. The window is revealed as the blinds are raised, and they can be raised to a height of 6.5 feet above the window's lower-most point. The window's uncovered area increases as the blinds' height increases.

Problem 1 (from class): Use a Riemann sum to define a function that approximates the uncovered area of window, expressed as a function of how high the blinds are above the window's bottom-most point.

Solution from class:

x = height of blinds above window's bottom, in feet

0 ≤ x ≤ 6.5

m = 200

h=.05

w(x) =

(Note: type ctrl-R to get "", the square root sign)

A(x) =

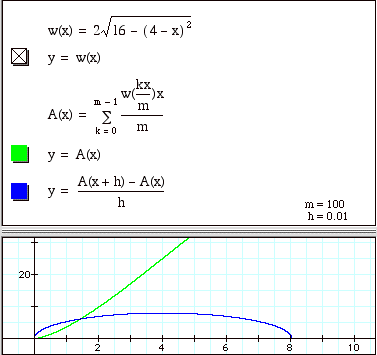
Problem 2 (from class): Construct a function that approximates the rate of change of uncovered area with respect to its height, where the function is expressed as a function of the blinds' height.

Solution from class:

A(x) =

r(x) =

Problem 3 (for you, now):

Why do the graphs of r(x) and w(x) appear to coincide?

(I'm looking for a conceptual explanationÑan explanation that makes clear what is going on.)