Introduction to Graphs
P. Thompson
Extended Analysis of Functions 1, Fall 2005
(Reprise of Saturday Math Club activity)
The main idea of this introduction is that we want children to envision three things:
1. to envision a graph as being a collection of points;
2. to envision the collection of points as being generated by keeping track, simultaneously, of two quantities whose values vary (or have varied or will have varied).
3. to envision that every point in a graph represents, at once, values of two quantities;
I did not treat these goals as "1, 2, and then 3". Rather, I treated 1 by itself, then 2 and 3 together.
A graph is a collection of points
I raise this issue by having children first make explicit the senses of "making a point" and "making a line". People typically think of making a point as making a dot with the tip of a pencil. This entails a very definite action with the hand, fingers, and forearm. People typically think of making a line by dragging a pencil with a sweep of the arm. The two actions (make a point and make a line) entail very different physical movements and hence lead to an intuition that when you make a line you don't make any points.
I employ two activities to counter children's thinking that you can draw a line without making any points. The first is to make it acceptable that drawing a line is a way to draw lots of points. I do this by asking children to make a point, then make 5 points along a line, then 10 points, then 20 points, then 30 points, then "make at least 1000 points along a line". It is then that I draw a line segment to suggest a way to make at least 1000 points.
Then I suggest we think about magnifying our view of any line segment we draw. ( I should have had magnifying glasses in class so that you could have done this; it is essential that you have them when you do this activity with schoolchildren.) You must emphasize that the purpose of doing this is to make everyone aware that what looks solid to the eye is, upon closer inspection, just a bunch of points.
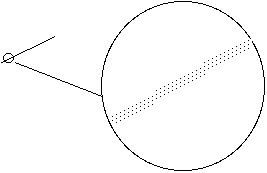
You might follow this activity by having them investigate photographs, newsprint, and so on to emphasize even more strongly that what looks solid at first glance is just a bunch of points.
Graphs are generated by keeping track simultaneously of two quantities as they vary
Here is what I did with you in class. I have a videotape of doing exactly the same activity with 6th-graders.
1. I had you keep track of Rabbit's total time running with your right hand. You picked a position on your desk that represented "0 seconds" and then you moved your finger sideways while Rabbit ran so that, at every moment of Rabbit running, the distance between your finger and "0" represented Rabbit's elapsed time.
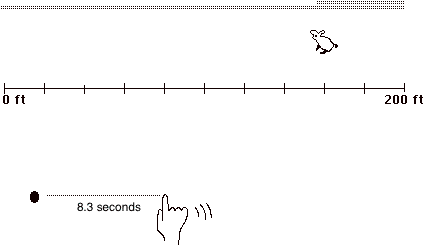
I paused Rabbit several times, asking you to say where you should look to see your representation of Rabbit's elapsed time (saying "NO" whenever I heard "look at your finger", saying "YES" whenever I heard anything like "look at the distance between your finger and where it started").
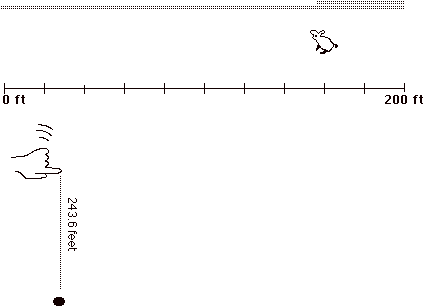
2. I had you keep track of Rabbit's total distance in very much the same way as you kept track of Rabbit's elapsed time. I asked you to raise your left index finger above your desktop so that the distance between your index finger and the desktop represented how far Rabbit has run.
3. I then had you keep track of the two simultaneously by doing both 1 and 2 at the same time.
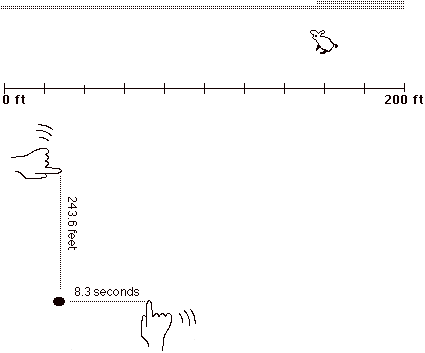
4. I then had you do the same thing as in 3, but you aligned your left finger so that it always was directly above your right finger.
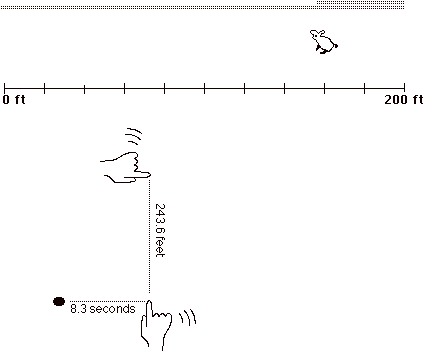
Every point in a graph represents, at once, values of two quantities
In the final phase, of this activity, I told you that I'd come into the room early and put a bowl of Fairy Dust on each of your desks. I asked you to imagine that you dip your finger into the Fairy Dust and wave your finger around, like Tinker Bell flying through the air, and to describe what you see (a trail of Fairy Dust). We discussed whether that trail was solid (no, it is made of particles of Fairy Dust)
I then asked you to dip your finger again into your bowl of Fairy Dust; we repeated Phase 4, as described above. We then talked about the "trail of Fairy Dust", what it resembled (a line), and what each particle of Fairy Dust represented (an amount of elapsed time together with how far Rabbit had run in that amount of time).
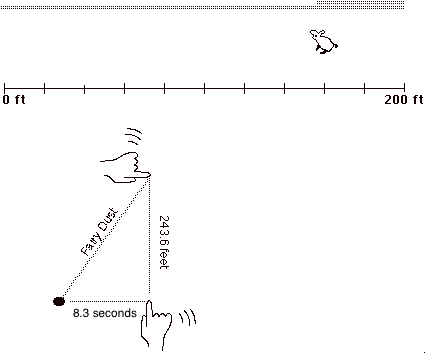
We repeated this several times, each time discussing what we had represented.