The following problems are from various texts. For some problems, if you approach them traditionally you will write an equation and solve for the variable in that equation. As you noted in class, in writing this equation you will be treating the variable as if it is a constant—it does not vary. Rather, it stands for “the answer”.
For other problems, if you approach them traditionally you will apply the techniques of the calculus, but still you would arrive at "the answer".
As such, please answer these questions for two of problems 2-7 (problem 1 is an example):
a) Describe how we can think of this problem so that it involves a functional relationship between covarying quantities. Write the functional relationships.
b) Phrase the problem's question so that the answer is a function.
c) Ask an additional question so that the answer to it is an answer to the original question. Answer that question.
d) Describe the difference in students' experiences between answering the question as originally posed and answering your revised question.
Example of setting up functional relationships and interpreting the graphs:
It
is 1873 in Territorial New Mexico. The Lone Ranger is chasing a desparate bank
robber over the desert. Both are on horseback, and the bank robber got an 11
mile head start. The bank robber's horse can run steadily at 16 miles per hour.
The Lone Ranger's horse can run steadily at 19 miles per hour. The bank robber
is heading for the Mexican border, for if he can cross the border he will be
safe. The town that they started from is 49 miles from the border. Will the
Lone Ranger catch the bank robber?
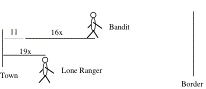
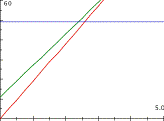
x = number of hours that have passed since LR began chasing the bandit.
f(x) = 19x This is the Lone Ranger's distance from town x hours after he started chasing the bank robber
g(x) = 16x + 11 This is the robber's distance from town x hours after the Lone Ranger started chasing him
h(x) = 49 This is the border's distance from town x hours after the Lone Ranger started chasing the bank robber.
|
|
- The graphs show the
robber's distance from town and the Lone Ranger's distance from town at each
moment after the Lone Ranger started chasing the robber.
- Any vertical distance
between ranger's and robber's graphs shows the distance between the two at that
moment during the chase.
- The horizontal graph
shows how far from town the border is at every moment during the chase.
- The vertical distance
between the ranger's and robber's graphs decreases as the number of hours they
have run increases, so the Lone Ranger is catching up to the robber.
- However, when the
robber hits the border (i.e., is 49 miles from town), the Lone Ranger is less
than 49 miles from town. The robber gets away (unless the ranger follows him
into Mexico).
Problems
1. A community group has 2000 perimeter-feet of prefabricated wall to build the superstructure for a single-story, rectangular convention hall. The hall needs to be further subdivided by two walls through its interior so that the hall is made of three huge rectangular rooms. What outer dimensions will give the convention hall as much floor space as is possible? (See a GSP sketch of this example and a Graphing Calculator example of an explained model.)
|
Figure 1 |
2. Bob drank 2/3L of water in 5/7 minute. In how many minutes will he drink 3/8L of water?
3. An A-frame barn is to be built so that it is 30 ft high, 40 ft wide and 60 ft long. A rectangular room is to be built inside the barn so that its ceiling abuts the roof. What dimensions will maximize the volume of the room?
4. You have a circle of radius 5 ft. Find the dimensions of the triangle circumscribed by this circle that has the largest possible area.
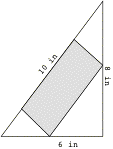
5. A rectangle is to be inscribed in a right triangle having sides of length 6 in, 8 in, and 10 in (Figure 1). Find the dimensions of the rectangle with greatest area assuming the rectangle has two vertices on the triangle's hypotenuse and one vertex on each of the other sides, as in the figure to the right.
6. Jamie Johnson rides frequently with her father to Chicago. On one particular trip it took 2 hours for them to travel the 110 miles from home to Chicago. They made the trip in two parts. Jamie kept an eye on the speedometer and estimated that in the first part they averaged 40 miles per hour. She estimated that in the second part they averaged 60 miles per hour. About how long did they drive in each part of the trip?
7. Statistical data from trucking companies suggests that the operating cost of a certain truck (excluding driver's wages) is 48+s/4 cents per mile when the truck travels at s miles per hour. If the driver earns $12.00 per hour, what is the most economical speed to operate the truck on a 400 mile turnpike where the minimum speed is 40 miles per hour and the maximum speed is 75 miles per hour?