Students often have a very hard time understanding inequalities and their solution sets. They often approach inequalities as if the idea is unrelated to everything they have done. This activity suggests one way to approach the idea of inequality so that what is conventionally proposed as an out-of-the-blue procedure instead emerges as a natural response to very sensible questions.
For them to understand the idea of inequalities and their solution sets, they must have a particular understanding of equations and variables.
Equations
How students understand equations is either the biggest obstacle or the biggest aid to their coherent understanding of inequalities.
|
3x2+2x-7 = 4
|
3x2+2x-7 < 4
|
|
| UNDERSTANDING OF EQUATIONS THAT POSES AN OBSTACLE |
IF students think of this equation as "the answer" being a number that hides behind the letter "x", and that his or her responsibility is to figure out what that number is, THEN
|
AS A RESULT they will likely think of " 3x2+2x-7 < 4" in a number of confusing ways:
|
|
|
|
|
| UNDERSTANDING OF EQUATIONS THAT IS SUPPORTIVE |
IF students think of this equation as an open sentence, a statement that is neither true nor false by itself, and becomes true or false as you replace x with various values, then
|
AS A RESULT they will likely think of this statement more coherently:
|
Inequalities
The following activity can be used to introduce students to the idea of inequalities. It begins with inequalities in two variables rather than inequalities in one variable. This is because the added complexity actually increases the level of interest students feel.
To do this activity you will need
- Graphing Calculator (3.0 or higher) from PacificTech.
- A clear overhead transparency sheet
- Scotch tape
- Transparency marker (erasable)
Tape the clear overhead transparency to your computer's screen.
The activity
Be sure to remind students of the meaning you already established for equations (see prior comments), the implied question, and what a solution set is.
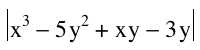
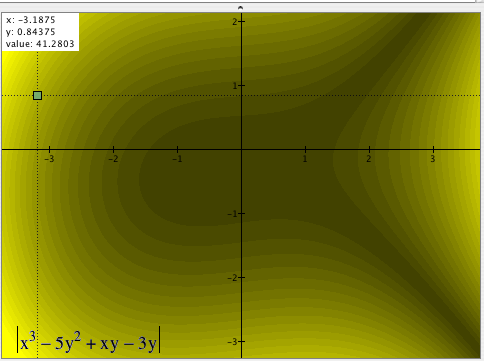
Click on the graph to get a GC file for this activity,
OR
- Type x3 - 5y2 + xy - 3y into Graphing Calculator (DO NOT press enter)
- Select Graph>Density Plot (i.e., in the Graph menu, select Density Plot
- Press Enter (or click Graph)
Lesson Logic (for you to complete)
| Step |
Action
|
Reason
|
| 1. | Discuss with students that the expression at the page's top is simply a calculation rule. It says what to do with values of x and y once they are given. You might give them several values of each for them to calculate. | You don't want students to think that you expect them to solve anything nor that you expect them to "know what x and y are". |
| 2. | Tell them to click anywhere on the graph (but not on an axis). Explain that where they clicked indicates a point in the coordinate plane, and that GC tells them the point's x-coordinate, its y-coordinate, and the value of the expression after substituting those values of x and y into it.
Have them click several places so that they can see that this is indeed how it works. |
This familiarizes them with the program's interface and builds confidence that this complicated formula can be evaluated easily for whatever values of x and y they choose. |
| 3. | Ask students to use their markers to indicate 5 points on the screen that have coordinates that make the expression have a value less than 6. |
... ... ... |
| 4. | (You complete the rest of this table) | |
| 5. | ||
| 6. | ||
|
.
. . |
.
. . |
.
. . |