The strategy is to make the correlation between the Predictor and Reputation as high as possible at every step of the way. So, the variable that correlates the highest with Reputation is the one that will predict Reputation best. So start with it. Then look for the next highest, etc.

Here are the correlations among the variables that are common to Colleges230 and to CollegesAll.

Pearson Product-Moment Correlation
	zRepu	zAcctRate	zGradRate	zTop10%	zTest75	zTest25
zRepu	1.000
zAccRate	-0.656	1.000
zGradRate	0.804	-0.600	1.000
zTop10%	0.746	-0.708	0.762	1.000
zTest75	0.812	-0.708	0.842	0.845	1.000
zTest25	0.825	-0.731	0.853	0.823	0.961	1.000

Notice that the correlations are the same whether we correlate z-scores or we correlate raw scores. Why? Because the formula for correlation converts every score to a z-score before summing the products, and the z-score of a z-score is itself. Click here for a more complete explanation.

Pearson Product-Moment Correlation
	Repu	AcctRate	GradRate	Top10%	Test75	Test25
Repu	1.000
AccRate	-0.656	1.000
GradRate	0.804	-0.600	1.000
Top10%	0.746	-0.708	0.762	1.000
Test75	0.812	-0.708	0.842	0.845	1.000
Test25	0.825	-0.731	0.853	0.823	0.961	1.000

The next table shows the steps I went through as I constructed my final Predictor formula, trying to make the highest possible correlation between Predictor and Reputation.

Variables in Predictor	C1	C2	C3	C4		r		Comment
zTest25	1.00					0.825		Started with zTest25 because it has highest correlation with Reputation.
zTest25, zTest75	1.00	0.40				0.828		Added zTest75 because it is next highest in correlation with Reputation. Varying C1 doesn't help; adding zTest75 doesn't help Even taking C2 to 0 decreases overall r, because zTest75 forces some missing values in Predictor that weren't there in just zTest25.
zTest25, zGradRate	1.00	1.00				0.849		Tried zGradRate because it is next highest in correlation with Reputation. Changing C1 still doesn't affect value of r.
zTest25, zGradRate, zTop10%	1.00	1.00	0.50			0.844		ZTop10% is next highest in correlation with Reputation. Notice that max value of r decreases.
zTest25, zGradRate, zAccRate	1.00	1.00	-0.25			0.855		Tried zAccRate because it was next highest in (absolute value of) correlation with Reputation.
zTest25, zGradRate, zAccRate, z%Ovr50	1.00	1.00	-0.25	0.50		0.880		Tried z%Ovr50 because it was next highest in correlation with Reputation. Notice that this is the biggest jump in r's value of any single addition. Why? Z%Ovr50 actually has a low correlation with Reputation. Why should it increase the correlation of Predictor and Reputation? Adding any variable other than z%Ovr50 resulted in a lower maximum value for r. DARN. z%Ovr50 is not in the CollegesAll data set, so I can’t use it to predict reputation scores for colleges in that data set.
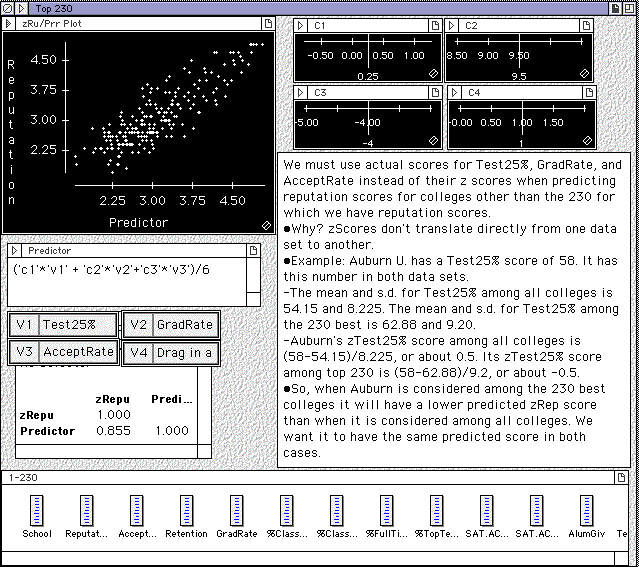
OOPS. I can’t include z scores in the equation I use for Colleges All. I have to use raw scores. We must use actual scores for Test25, GradRate, and AcceptRate instead of their z scores when predicting reputation scores for colleges other than the 230 for which we have reputation scores. Why? zScores don't translate directly from one data set to another.
Example: Auburn U. has a Test25% score of 58. It has this number in both data sets. The mean and s.d. for Test25 among all colleges is 54.15 and 8.225. The mean and s.d. for Test25% among the 230 best is 62.88 and 9.20. Auburn's zTest25 score among all colleges is (58-54.15)/8.225, or about 0.5. Its zTest25 score among top 230 is (58-62.88)/9.2, or about -0.5. Put another way, a zScore's value is relative to the dataset containing that score. Change the data in the set so that the mean and standard deviation change and the set's zScores will change.
When Auburn is considered among the 230 best colleges it will have a lower predicted zRep score than when it is considered among all colleges. We want it to have the same predicted score in both cases.
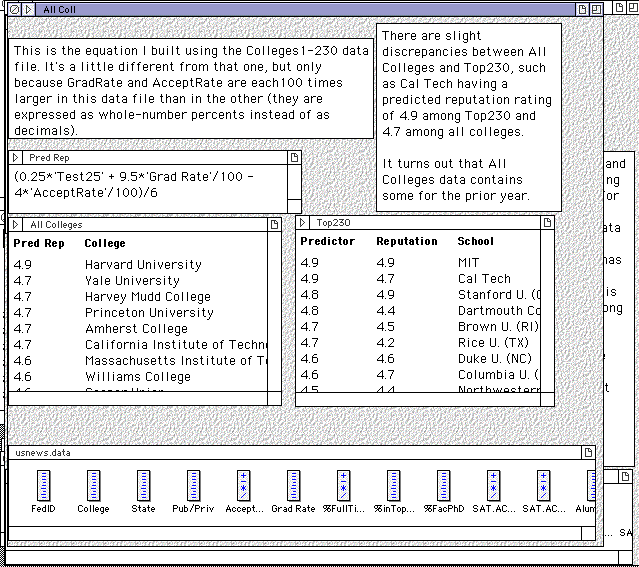
I then put Test25, GradRate, and AccRate (instead of the zScore versons) into Predictor and adjusted the coefficients at each step to get the correlations I’d already found with the zScore variables.
Predict Actual Reputations with this formula:												In Colleges All data, predict reputation scores with this formula: