Parametric Functions

We have actually been employing the idea of parametric functions all along but have not named it. We called it, "Keeping track of two quantities' values simultaneously." We did that in the Cities A and B activity, where we kept track of a car's distances from City A and from City B simultaneously.

We also employed the idea of paramatric functions in every graphing activity in which we kept track simultaneously of a variable's value and the value of a function defined in terms of that variable's value. We did this when we

• modeled concrete situations,
• analyzed the behavior of functions,
• defined angle measure and trig functions, and issues about trig function's behaviors,
• graphed functions in polar coordinates,
• kept track of how fast quantities changed, how much they accumulated, and how fast their accumulations changed.

Activity 1

The graphic below shows the graphs of sin(2x) and cos(x) on the same coordinate system. As an exercise (in the spirit of City A and City B), do this:

Activity 2

Predict the graph of 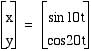. Check yourself by clicking here.